Discrete topology and geometry refresh our understanding in intrinsic Hall effects
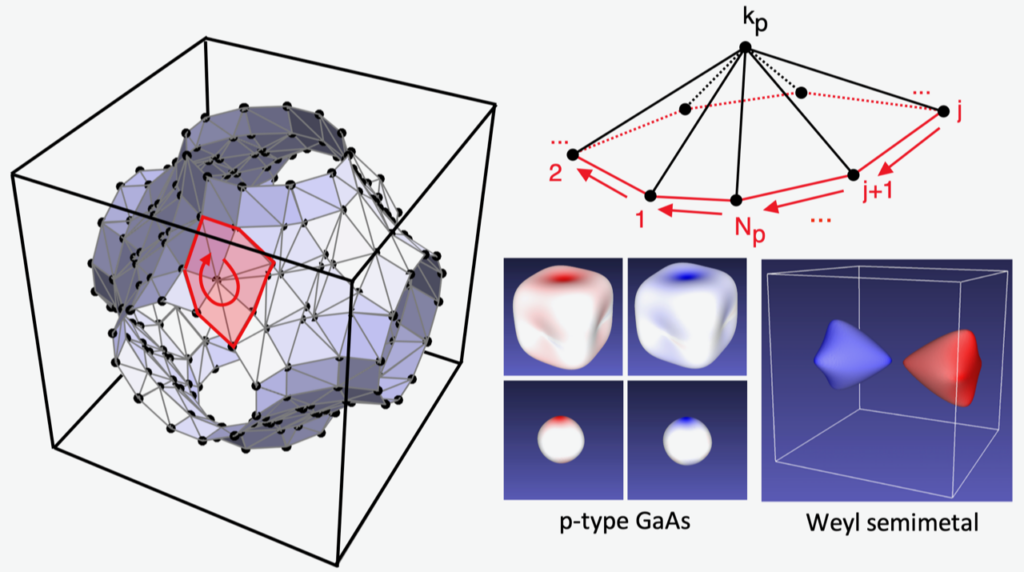
A recent work by Prof. Gen Yin and collaborators identified a new perspective to resolve the k-space quantum geometry on the vertices of Fermi surfaces. Such new approach naturally handles the singularity issue of the conventional Berry curvature integration, and enables the theoretical evaluation of intrinsic Hall effects resolved in arbitrary local properties of the Fermi surface such as the electron spins. The new approach is stable against Kramers degeneracy, and is particularly useful for materials with strong spin-orbital couplings. Read more details at: Phys. Rev. B 104, 184408 (2021).